Solución sistema ecuaciones método de Gauss-Jordan
Solución sistema ecuaciones método de Gauss-Jordan
Método de eliminación de Gauss
Consiste en operar sobre la matriz ampliada del sistema, hasta hallar la matriz triangular superior.
Recordemos que la matriz triangular superior, es una matriz de la forma:
La matriz ampliada resulta de tomar los coeficientes de las variables de un sistema de ecuaciones cuadrado, más el valor de sus términos independientes, es decir, suponga el siguiente sistema de ecuaciones:
Se puede observar que cada elemento de la matriz, coincide con los coeficientes de las variables y en donde la columna 4, será los valores para los términos independientes.
Una vez se tenga la matriz ampliada, se procede a dejar la expresada como una matriz escalonada o triangular superior. Cuando se consiga esto, se va evaluar el valor de la posición 3.3 respecto a la 3.4, para poder despejar el valor de la z o la tercera variable del sistema. Dependiendo del resultado, se debe seguir subiendo en las filas, para poder despejar el valor de las demás incógnitas.
Según lo previamente dicho, z = 3, podría reemplazar z en la nueva expresión, y + 3z = 7 (y = -2), para poder despejar y finalmente, teniendo los valores para y y z, despejar la x.
Método Gauss-Jordan
Como tal, este método es una versión ampliada del método de Gauss. Consiste en convertir la matriz inicial en la matriz identidad, en donde los valores 1 de la diagonal principal, corresponderán en orden a x, y y z.
Matriz identidad
Extraído: economipedia.com
Es decir, se generan los mismos pasos que en el método de Gauss, pero en lugar de hallar la matriz triangular superior, hallamos la matriz identidad.
extraído: matemáticas profe Alex
La gran ventaja del método de Gauss-Jordan es obtenemos de manera directa los valores de las incógnitas y no tenemos que ir reemplazando y despejando variables, luego de hacer las operaciones con matrices




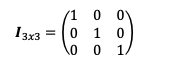



Comentarios
Publicar un comentario